
We prove in particular that this projection is a locally trivial C ∞ fibration if X is modular, and deduce some exact sequences involving the fundamental groups of the complements of A, of A /X, and of some (affine) arrangement A z 0 X. The Hyperplane Arrangement Problem The Intersection Poset and Characteristic Polynomial De nition De ne theintersection posetof an arragement Ain V Kn, denoted L(A), as the set of all non-empty intersections of sets of hyperplanes B 2Aordered by reverse inclusion. 4, we study in detail the hyperplane arrangements corresponding to hook diagrams. Our study starts with an investigation of the projection p :M( A )→M( A /X) induced by the projection C n → C n /X. The essentialization of a hyperplane arrangement whose base field has characteristic 0 is obtained by intersecting the hyperplanes by the space spanned by their. the intersection of the coordinate arrangement in a larger space with the subspace corresponding to. As such, the intersection poset of a central hyperplane arrangement is. (3) the centralizer is equal to the direct product of π 1 (M( A X )) and the center of π 1 (M( A X )). Any finite meet semilattice with a maximum element 1 is a lattice, for the least. Well this is a lattice, in zero dimensions. Let 1 generate a lattice in R1, and let generate another lattice in R1. (2) the normalizer is equal to the commensurator and is equal to the direct product of π 1 (M( A X )) and π 1 (M( A X )) The intersection of two lattices is often another lattice, though it might live in a lower dimension. Diaprés la prop.riété 11 et le théorème 2 (Conf. Such regret functions can be defined on any convex set but if a sufficiency condition is added the regret function must be proportional to information divergence and the convex set must be spectral. i s il suffit qu il o) Prenons le cas treillis géométrique de dimension finie. For convex optimization problems Bregman divergences appear as regret functions. Je vais établir la réciproque s THÉORÈME 3 - pour treiljl.

For X in L ( A ) we set A X = and π 1 (M( A X )) is included in the centralizer of π 1 (M( A X )) in π 1 (M( A )) Cette propriété est encore équivalente à la suivante s H étant un hyperplan, A B entraine il n E) B (A On en déduit qu un treillis géométrique modulaire est projectif. For the basic facts about posets and lattices we are using here, see ref.
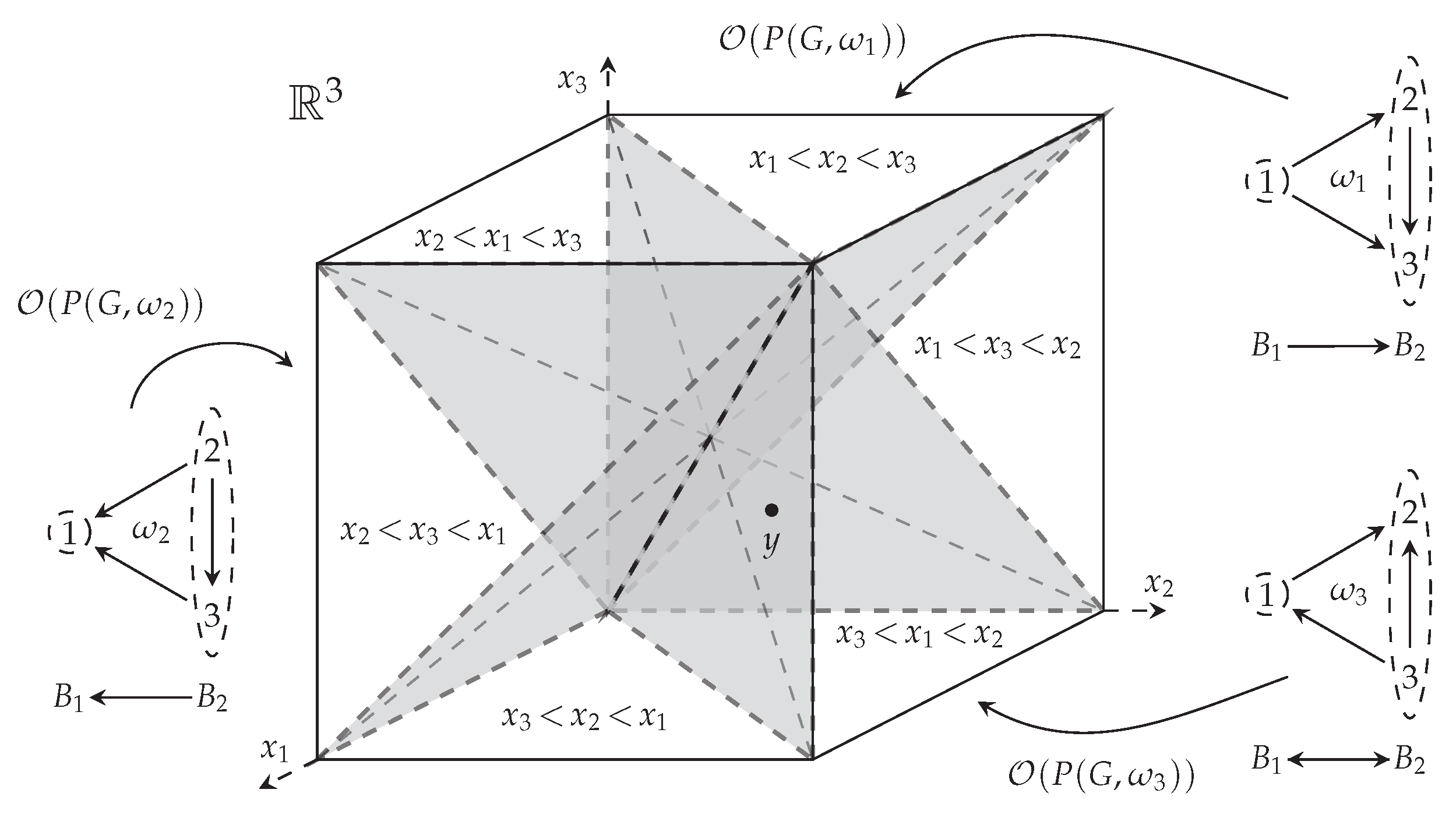
Let A be a central arrangement of hyperplanes in C n, let M( A ) be the complement of A, and let L ( A ) be the intersection lattice of A. lattice) if and only if the intersection of all the hyperplanes in si is nonempty.


 0 kommentar(er)
0 kommentar(er)
